텍스트마이닝 이진분류(랜덤포레스트), 머신러닝 비지도학습 LDA
디리클레.. 처음 들어봤습니다.
조선시대 성종 때 얘깁니다.
정희량이 갑자사화를 피하려 은둔생활을 할 때
보통 문제는 요런 걸 드리는데, 갑자사화 ..

처음 들어봤습니다..
처음들어보셨나요?

오늘 적을 공부 내용은 살면서 처음 들어본
Machine Learning중, 비지도 학습인 LDA
Latent Dirichlet Allocation
직역하자면
(잠재의) (디리클레) (할당)
입니다.
“디리클레”는 사람이름이에요
토픽모델링 중 하나인데
토픽모델링(Topic Modeling)
기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법
출처: 위키 독스
라는데
"디리클레 할당"을 통해서 해당 문서의 관계어를 추출해 내는 기계 학습 기법 입니다.
배운게 아니라서
이 방법이 뭔지 공부하려고 여러 영상을 찾아봤는데요
- 풀로 다 본 것
유튜브 LDA Paper Review
- 이해가 안되서 훑어 본 것
유튜브 Topic Modeling Part2 (LDA Document generation process)
한국말인데 이해를 못하겠다는 점.
고려대에서 석사 중이셨던 발표자: 석사과정 윤훈상 님의
영상(첫 번째 영상임)을 여러번 듣고 최대한 풀어써보자면

일단 영단어부터 공부하고 가겠습니다
Distribution : 분포(젤 많이 나옴)
Parameter: 매개변수
Multinomial: 다-항의(항이 많아요)
mixture: 혼합된 어떤 것(명사임)
α: 알파, 그냥 그리스 문자(별 거 아님)
θ: 세타, 그냥 그리스 문자(숫자로는 9를 뜻함, 별거 아니에요)

문서의 단어 갯수 N = 포아송분포(보통은 생략, 잘 몰라도 됨)
디리클레 분포의 θ(세타) = Topic mixture(알파)
이렇게 이해하라는 선생님의 설명

mixture란 뭘까.. Topic A의 분포와 Topic B의 분포와 Topic C의 분포가 다 합쳐진 분포를 mixture 모델이라고 보면 됨.

("모르면 외워" 방식으로 접근)
Mixture Model은
전체 집단에서 하위집단을 찾는 것에 목적.
하위집단에 대한 통계적 추론을 하기 위함.
GMM(가우시안 믹스처 모델)이랑 비슷. 클러스터링과 유사하다는 석사과정: 유훈상님의 설명
Mixture Distribution은
하위집단에서 전체 집단 특징을 얻는 과정임.
LDA의 보충설명이란 느낌(스을슬 이해를 못하기 시작)

그래서 LDA의 과정이 뭐냐?
단순하게 다항 분포의 분포라고 보면 된다. (맨 밑의 짤 참고)
k = 3(토픽이 3개)인 확률 분포에 대한 분포?
3개의 확률변수에 대한
Multinomial distribution(다항 분포)이라고 했을 때
(0.7, 0.1, 0.2)
(0.6, 0.3, 0.1)
이걸 모조리 담고 있는게 디리클레 분포다.
k = 3 (토픽이 3개)에 대한 확률 분포를 dirichlet distribution으로 가져온다란 뜻은
distribution에서
topic1이 선택될 확률이 0.7
topic2가 선택될 확률이 0.15
topic3이 선택될 확률이 0.15이다
이게 mixture model에서의 가중치 역할이다.
그래서

mixture model에서 토픽 각각의 확률이 나타나는 것이다.
또,
3차원(k = 3) 디리클레 랜덤 변수인 세타는 (k-1)의 simplex이다.
근데 여기서 simplex가 무엇이냐?
쉽게 말하면 공간을 표현하는 방법임.
simplex가 3이면 삼각형
simplex가 2이면 선
마지막 줄의 의미는 LDA에서는 같은 알파인 dirichlet parameter를 사용한다는 것.
10 10 10
이렇게
그래서 세타 값이 같을 수 밖에 없음.
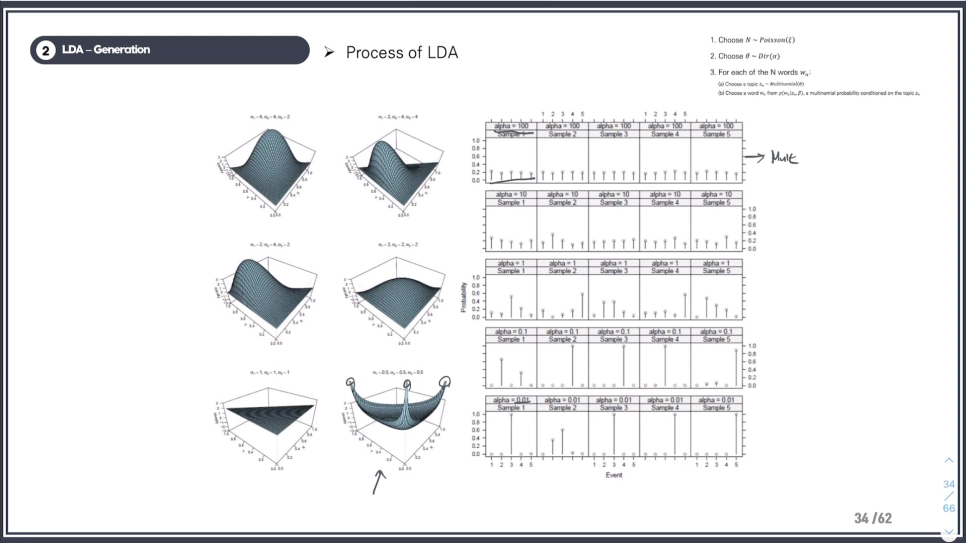
3차원 그래프를 자세히 보면
0.5 0.5 0.5로 하면 각 multinomial(다항분포)에 대한, 다른 말로 구성요소에 대한 개별 확률이 높아짐
2 2 2 일 때: 중앙에 몰려있어서 확률 분포가 균등하다
(뭔 말인지 모르겠다)

그나마 이해가 다시 되는 부분
각 Topic A, Topic B, Topic C
에서 distribution이 높은 Topic C가 뽑힌다.
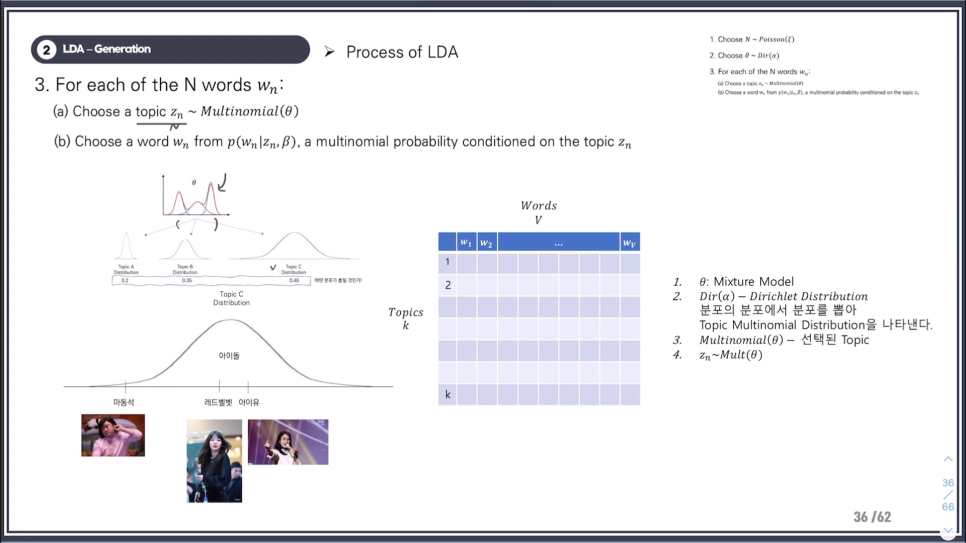
그래서 7시 방향의 그래프를 보면
아이돌이라는 토픽에서는 마동석이 잘 뽑히지 않는다
에스파, 르세라핌 같은 키워드가 뽑힐 확률이 높다.
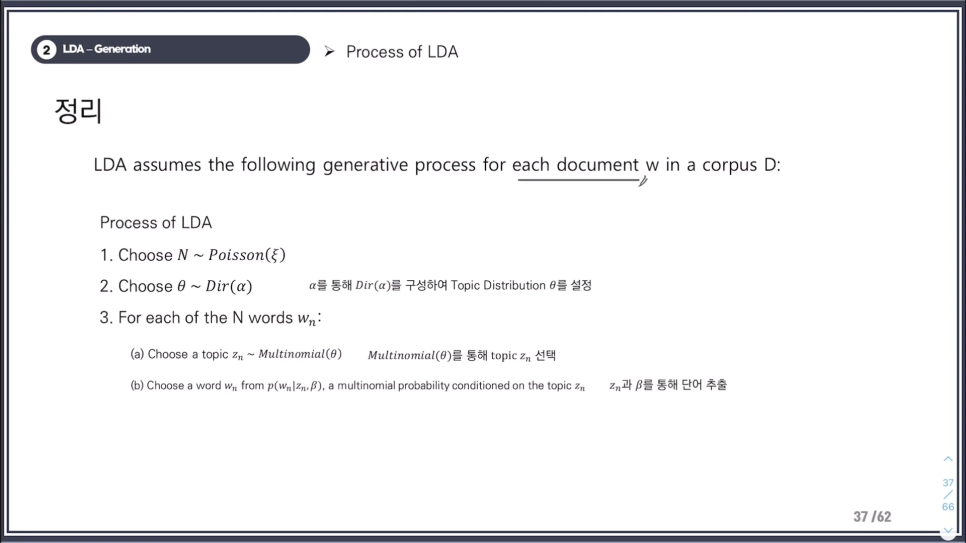
LDA에서 각각의 문서는 여러개의 주제를 가지고 있다. 확률 잠재 의미 분석 (Probabilistic latent semantic analysis, pLSA) 와 비슷하지만 주제들이 디리클레 분포를 따른다고 가정한다.
예를 들어 [양자역학, 힉스 입자, 맥스웰 방정식, 상대성 이론, 불확정성 원리]등의 단어들이 많이 쓰인 문서와 [셰익스피어, 톨스토이, 파우스트, 1984]등의 단어들이 많이 쓰인 문서가 있다고 해보자.
우리는 첫번째 문서가 물리학에 관련된 내용이고, 두번째 문서가 문학에 관련된 내용으로 추측할 수 있다.
그 이유는 우리는 문서에 들어가 있는 단어들이 해당 해당 주제들을 표현하고 있음을 알기 때문이다.
이러한 사전 정보가 없다면 주제를 예측할 수 없다. 하지만 사전정보가 없어도 단어들과 주제들은 연관성이 있다. 주제는 의미나 인식으로 결정되는 것이 아니고, 지도 학습으로 라벨링된 단어들의 가능도로 결정된다.
출처: 위키백과 https://ko.wikipedia.org/wiki/%EC%9E%A0%EC%9E%AC_%EB%94%94%EB%A6%AC%ED%81%B4%EB%A0%88_%ED%95%A0%EB%8B%B9
위의 설명을 토대로
하나의 corpus(?말뭉치가 맞는지는 모르겠습니다)에서 여러가지 주제의 문서가 있을 때
corpus를 LDA에 학습시키면
Topic 1
양자역학, 힉스 입자, 맥스웰 방정식, 상대성 이론, 불확정성 원리
Topic 2
셰익스피어, 톨스토이, 파우스트, 1984
Topic 3
파이리, 치코리타, 피츄, 몬스터볼
등(요건 설정할 수 있음)
이렇게 출력된다는 겁니다.
그래서 그걸 읽은 사람은
Topic1은 '아? 물리학에 관한 내용이구나'
Topic2는 '소설에 관한 이야기구나'
라고 알 수 있는 원리.
해당 토픽의 관계어들이 얼마나 관계가 있는지를 디리클레 할당으로 계산한다는 것.
(점수도 산출할 수 있어요)

(그럼 Topic 3는 뭘까요? )
공부한 내용을 사용해본 프로젝트 진행 상황
저희 팀은
- 20대·30대 위주의 좀 핫한 것들을 보여주는 서비스를 만들자
- 머신러닝을 써야한다
- 뉴스를 사용해보자
- 뉴스에 더해서 텍스트를 활용할 수 있는게 뭐가 있을까
이렇게 전개 됐슴다.
이걸 사용하면 커뮤니티의 hot한 것 들 제공 가능!
수업에서 공부한게 아니라서 계속 긴가 민가 한 상황 하지만 ?
돌려봤더니

과정 (불필요한 과정은 생략)
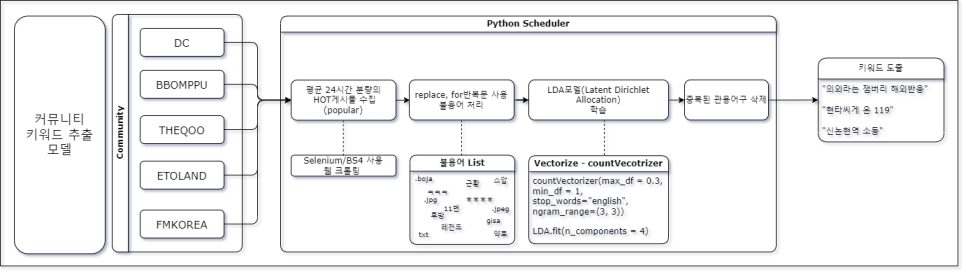
이 과정에서 판단이 필요했던 부분
- 일주일치 커뮤니티글 데이터를 학습. 학습된 lda를 통해 당일 데이터를 transform할 것인가?
- 커뮤니티글을 특정 시간 기준으로 매일 수집해서 학습시킬 것인가?
였는데요
1번으로 시작했는데, 커뮤니티는 최신 정보가 생명인데, 일주일 전 글들만 나오더라구요
vectorizer = CountVectorizer(max_df = 0.6, min_df = 2, stop_words="english", ngram_range=(2, 3))
X = vectorizer.fit_transform(synthesis)
#LDA 모델 학습
num_topics = 7 # 원하는 토픽의 수 설정
lda_model = LatentDirichletAllocation(n_components=num_topics, random_state= 42)
lda_model.fit(X)
당시 이미 맨시티는 한국 투어 경기도 마친 상태였는데, 요런 지난 글들이 아직까지 나오길래 1번 탈락
그래서 매일 당일 약 2000개 내의 커뮤니티 제목을 수집해서 매일 학습시키기로 결정했슴다
그 후 파라미터 조정을 거쳤는데요.
바로 GridSearch
가장 중요한 건 n_gram이듯 싶었습니다.
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import GridSearchCV
# countVec과 LDA묶기
lda_pipe = make_pipeline(CountVectorizer(), LatentDirichletAllocation())
# gridSearch해볼 parameter값들 적어넣기
param_grid = {
'countvectorizer__max_df': [0.3, 0.4, 0.5],
'countvectorizer__ngram_range': [(1, 2), (2, 2), (2, 3), (3, 3), (3, 4)],
'latentdirichletallocation__n_components': [4, 5, 6, 7, 8]
}
# cv=3으로 교차유효성검사를 3번으로 나눠서 한다
grid = GridSearchCV(lda_pipe, param_grid, cv=3)
grid.fit(X_train)
grid.best_params_출력 결과
{'countvectorizer__max_df': 0.3,
'countvectorizer__ngram_range': (3, 3),
'latentdirichletallocation__n_components': 4}일단 n_gram을 직접 조정해서 적게 했을 때
제목들이 쓰다 말아서 조금 아쉬웠고
최소 (3, 3) (3, 4)는 됐어야 했다고 생각했습니다.
이후 연관어들이 출력됐을 때 중복을 제거하는 코드를 집어 넣고 python파일로 저장.
이후 해당 파일 실행하면 컨텐츠가 출력ㄱㄱ
#해당 dataFrame에서 열 한 개를 list로 가져오기
daily_all_commu = daily_all_commu.loc[:, "content"].to_list()
# 불용어 지정. 많으면 많을 수록 좋을 듯
stopwords = ['-', 'jpg', 'ㅋ', '[ㅇㅎ]', "gif", '스압', 'ㅇㅎ', 'ㄷ', "ㅎ", ';', 'twt', 'blind', 'pann', 'gisa', '★', '☆', 'ㅠ', 'ㅜ', "manhwa", "mp4", "후방", "레전드", "주의", "JPG", 'webp', "boja"]
# 불용어가 제거된 데이터를 저장할 새로운 리스트
filtered_list = []
for item in daily_all_commu:
for stopword in stopwords:
item = item.replace(stopword, '')
filtered_list.append(item.strip())
# 총 데이터 갯수 확인
print(len(filtered_list))
# vectorizer와 lda모델 학습
vectorizer = CountVectorizer(max_df = 0.3, min_df = 1, stop_words="english", ngram_range=(3, 3))
X = vectorizer.fit_transform(filtered_list)
#LDA 모델 학습
num_topics = 6 # 원하는 토픽의 수 설정
lda_model = LatentDirichletAllocation(n_components=num_topics, random_state= 42)
lda_model.fit(X)
# 중복제거하지 않은 토픽들 list
keyword_li= []
# display 토픽 보여주기
def display_topic_words(lda_model, feature_names, num_top_words):
for topic_idx, topic in enumerate(lda_model.components_):
# Topic별로 1000개의 단어들(features)중에서 높은 값 순으로 정렬 후 index를 반환해줌
# argsort()는 default가 오름차순(1, 2, 3,..) 그래서[::,-1]로 내림차순으로 바꾸기
topic_word_idx = topic.argsort()[::-1]
top_idx = topic_word_idx[:num_top_words]
# CountVectorizer 함수 할당시킨 객체에 get_feature_names()로 벡터화시킨 feature(단어들) 볼 수 있음.
# 이 벡터화시킨 단어들(features)은 숫자-알파벳순으로 정렬되며, 단어들 순서는 fit_transform시키고 난 이후에도 동일!
# "문자열".join함수로 특정 문자열 사이에 끼고 문자열 합쳐줄 수 있음
feature_concat = " ".join([str(feature_names[i])+""for i in top_idx[:2]])
keyword_li.append(feature_concat)
feature_names = vectorizer.get_feature_names_out()
display_topic_words(lda_model, feature_names, 15)
# 중복제거한 키워드들 담을 = keyword_list
keyword_list = []
for lii in keyword_li:
uniq = list(lii.split(" "))
senten = " ".join(q for q in list(dict.fromkeys(uniq)))
keyword_list.append(senten)
print(keyword_list)그랬더니

정치적이거나 민감한 주제는 모자이크 처리 했습니당

프로젝트를 위한 워드클라우드 만들기
import matplotlib.pyplot as plt
from wordcloud import WordCloud
from collections import Counter
# 가장 많이 올라온 글들을 텍스트 리스트로 가져온다고 가정합니다.
font_path = './NanumSquareRoundR.ttf'
# 텍스트 리스트를 공백으로 구분된 하나의 문자열로 변환합니다.
text = " ".join(filtered_list)
# 단어 빈도수를 계산합니다.
word_counts = Counter(text.split())
# 가장 많이 등장한 단어 5개를 제외한 단어들을 가져옵니다.
top_words_to_exclude = [word for word, _ in word_counts.most_common(9)]
filtered_text = " ".join(word for word in text.split() if word not in top_words_to_exclude)
# WordCloud 객체를 생성하고 워드클라우드를 생성합니다.
wordcloud = WordCloud(width=1200, height=800, font_path=font_path, background_color='white').generate(text)
# 워드클라우드를 시각화합니다.
plt.figure(figsize=(15, 10))
plt.imshow(wordcloud, interpolation='bilinear')
plt.axis("off")
plt.show()말투가 어디서 본 것 같지 않나요?
네^^ 맞아요. GPT말투에요~

이렇게 LDA를 공부해봤는데요
외부 컨설팅 받을 때마다, 머신러닝이든 딥러닝이든 인공지능 공부하려면 석·박사 가라고 하는 말이 이해가 됩니다!
개어려워요
짤은 상업적 이용 목적이 아닙니다
차마 진지한 내용에 못 넣었던 짤
단순하게 "다항 분포의 분포"라고 보면 된다.

다항분포!


~의 분포!
2020년도에 석사하시고 계시던 윤훈상님 감사합니다
gpt도 2025년에 파산한다는 썰이 있던데 얼른 유료 결제 가보자고
암튼 끄읏!
'아카이빙 > (구) 인사교 교육들과 정보처리기사' 카테고리의 다른 글
| 2023 인공지능사관학교 이미지처리 OpenCV, Tesseract (0) | 2024.11.22 |
|---|---|
| 2023 인공지능사관학교 딥러닝 공부 (1) | 2024.11.18 |
| 2023 인공지능사관학교 안드로이드 intent (2) | 2024.11.18 |
| 정보처리기사 실기 2023. 8. 24. C출력문, Java 자료형 (0) | 2024.11.13 |
